P值计算器
使用此 p 值计算器计算给定 z 分数的右尾、左尾或双尾 p 值。它还会在表示 p 值的区域中生成法线和阴影。 要使用计算器,只需输入标准正态分布的 z 得分,选择 p 值类型,然后单击“计算”按钮即可生成结果。
Right-tailed p-value: P(Z > z) = 0.0668072
欢迎使用我们的p值计算器!您再也不用想知道如何找到 p 值,因为在这里您可以根据所有最流行的分布从检验统计量中确定单侧和双侧 p 值:正态分布、t-Student、卡方分布和 Snedecor's F。
什么是 p 值?
从形式上讲,p 值是检验统计量生成值的概率,其极端值至少与其为样本生成的值一样极端。重要的是要记住,这个概率是在原假设为真的假设下计算的!
更直观地说,p值回答了这个问题:
假设我生活在一个零假设成立的世界里,对于另一个样本,我正在执行的测试产生的值至少与我对已有样本观察到的值一样极端的可能性有多大?
它是确定“极端”实际含义的备择假设,因此 p 值取决于您陈述的备择假设:左尾、右尾或双尾。在下面的公式中,代表检验统计量,对于它为给定样本产生的值,并且是事件的概率,在假设 HSxPr(event | H0)0是真的:
-
左尾测试:
p-value = Pr(S ≤ x | H0) -
右尾测试:
p-value = Pr(S ≥ x | H0) -
双尾测试:
p-value = 2 * min{Pr(S ≤ x | H0), Pr(S ≥ x | H0)}(Bywe 表示较小的数字 outand。
min{a,b}ab如果检验统计量的分布在 H0对称约为 0,则
p-value = 2 * Pr(S ≥ |x| | H0)或者,等效地,
p-value = 2 * Pr(S ≤ -|x| | H0)
由于一张图片胜过千言万语,让我们来说明这些定义。在这里,我们使用的事实是,概率可以整齐地描述为给定分布的密度曲线下的面积。我们给出了两组图片:一组用于对称分布,另一组用于偏斜(非对称)分布。
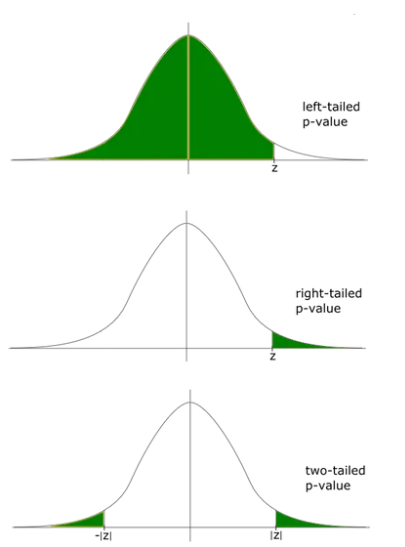
- 对称情况:正态分布
- 非对称情况:卡方分布
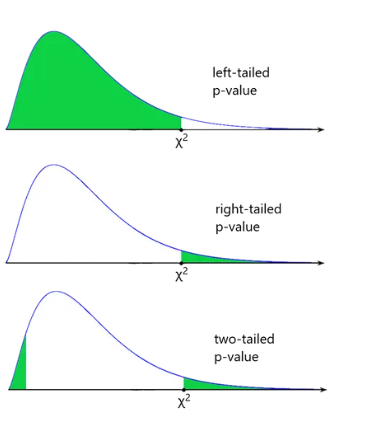
在最后一张图片(偏态分布的双尾 p 值)中,左侧的面积等于右侧的面积。
如何根据检验统计量计算 p 值?
要确定 p 值,您需要知道假设原假设为真的检验统计量的分布。然后,借助该分布的累积分布函数 (),我们可以表示检验统计量至少与其样本值一样极端的概率:cdfx
-
左尾测试:
p-value = cdf(x) -
右尾测试:
p-value = 1 - cdf(x) -
双尾测试:
p-value = 2 * min{cdf(x) , 1 - cdf(x)}如果检验统计量的分布在 H0在0 左右对称,则双侧 p 值可以简化为 ,或者等效地为
p-value = 2 * cdf(-|x|)p-value = 2 - 2 * cdf(|x|)
假设检验中最普遍的概率分布往往具有复杂的 cdf 公式,并且可能无法手动查找 p 值。您可能需要求助于计算机或统计表,人们在其中收集了近似的 cdf 值。
好吧,您现在知道如何计算 p 值,但是...为什么首先需要计算这个数字?在假设检验中,p 值方法是临界值方法的替代方法。回想一下,后者要求研究人员预先设定显著性水平,α,即当原假设为真时拒绝原假设的概率(因此类型I错误)。获得 p 值后,只需将其与任何给定α进行比较,即可快速决定是否在该显著性水平(α)否定原假设。有关详细信息,请查看下一节,我们将在其中解释如何解释 p 值。
如何解释 p 值?
正如我们上面提到的,p 值是以下问题的答案:
假设我生活在一个零假设成立的世界里,对于另一个样本,我正在执行的测试产生的值至少与我对已有样本观察到的值一样极端的可能性有多大?
这对你来说意味着什么?好吧,您有两种选择:
- 较高的 p 值意味着您的数据与原假设高度兼容;和
- 较小的 p 值可提供反对原假设的证据,因为这意味着如果原假设为真,则结果将非常不可能。
但是,原假设可能为真,但您的样本非常不寻常!例如,假设我们研究了一种新药的效果,并得到了 p 值。这意味着,在类似的研究中,随机机会本身仍然能够产生我们获得的测试统计量的值,或者更极端的值,即使药物根本没有效果!0.033%
“什么是 p 值”这个问题也可以回答如下:p 值是拒绝原假设的最小显著性水平。因此,如果您现在想在某个显著性水平上对原假设做出决策,只需将您的 p 值与以下值进行比较:αα
-
如果,则您拒绝原假设并接受备择假设;和
p-value ≤ α -
如果,那么你没有足够的证据来否定原假设。
p-value ≥ α
此外,请记住,学科领域的专业知识(和共同原因)至关重要。否则,盲目地应用统计原理,你可以很容易地得出
如何使用 p 值计算器从检验统计量中查找 p 值?
由于我们的 p 值计算器随时为您服务,您不再需要想知道如何从所有这些复杂的检验统计数据中找到 p 值!以下是您需要遵循的步骤:
-
选择备择假设:双尾、右尾或左尾。
-
告诉我们您的检验统计量在原假设下的分布:是 N(0,1)、t-学生、卡方还是 Snedecor 的 F?如果您不确定,请查看以下部分,因为它们专门介绍这些发行版。
-
如果需要,请指定检验统计量分布的自由度。
-
输入为数据样本计算的检验统计量值。
-
我们的计算器根据检验统计量确定p 值,并提供要对原假设做出的决策。默认情况下,标准显著性水平为 0.05。
如何从 z 分数中找到 p 值?
-
左尾 z 检验:
p-value = Φ(Zscore) -
右尾 z 检验:
p-value = 1 - Φ(Zscore) -
双尾 z 检验:
或p-value = 2 * Φ(−|Zscore|)
p-value = 2 - 2 * Φ(|Zscore|)
如果检验统计量近似于标准正态分布 N(0,1),则使用Z 分数。多亏了中心极限定理,如果你有一个大样本(比如至少 50 个数据点),你可以指望近似值,并将你的分布视为正态分布。
Z 检验通常是指检验总体均值或两个总体均值之间的差异,尤其是两个比例之间的差异。您还可以在最大似然估计中找到 Z 检验。
如何从 t 中找到 p 值?
t得分的 p 值由以下公式给出,其中代表具有自由度的 t-Student 分布的累积分布函数:cdf==t,d==d
-
左尾 t 检验:
p-value = cdft,d(tscore) -
右尾 t 检验:
p-value = 1 - cdft,d(tscore) -
双尾t检验:
或p-value = 2 * cdft,d(−|tscore|)
p-value = 2 - 2 * cdft,d(|tscore|)
导致χ²分数的最流行的测试如下:
-
测试正态分布数据的方差是否具有某个预定值。在这种情况下,检验统计量具有具有自由度的 χ² 分布,其中样本数量。这可以是单尾或双尾测试。
n - 1n -
拟合优度检验检查经验(样本)分布是否与某些预期概率分布一致。在这种情况下,检验统计量服从具有自由度的 χ² 分布,即样本划分为的类数。这是一个右尾测试。
k - 1k -
独立性检验用于确定两个变量之间是否存在统计显著关系。在这种情况下,其检验统计量基于列联表,并服从具有自由度的 χ² 分布,其中行数和列数是此列联表中的行数和列数。这也是一个右尾测试。
(r - 1)(c - 1)rc
卡方得分的 p 值(χ2 分数)
在执行检验统计量服从χ² 分布的检验时,请使用该选项。
例如,如果您取平方变量的总和,每个变量都遵循正态分布 N(0,1),则会出现这种分布。请记住检查检验统计量的 χ² 分布的自由度数!χ²-score
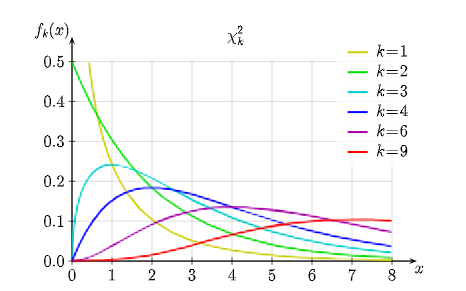
如何从卡方分数中找到 p 值?您可以借助以下公式来做到这一点,其中表示具有自由度的 χ² 分布的累积分布函数:cdfχ²,dd
-
左尾χ²检验:
p-value = cdfχ²,d(χ²score) -
右尾χ²检验:
p-value = 1 - cdfχ²,d(χ²score)请记住,拟合优度和独立性的 χ² 检验是右尾检验!(见下文)
-
双尾χ²检验:
p-value =2 * min{cdfχ²,d(χ²score), 1 - cdfχ²,d(χ²score)}(Bywe 表示较小的数字和。
min{a,b}ab
导致χ²分数的最流行的测试如下:
-
测试正态分布数据的方差是否具有某个预定值。在这种情况下,检验统计量具有具有自由度的 χ² 分布,其中样本数量。这可以是单尾或双尾测试。
n - 1n -
拟合优度检验检查经验(样本)分布是否与某些预期概率分布一致。在这种情况下,检验统计量服从具有自由度的 χ² 分布,即样本划分为的类数。这是一个右尾测试。
k - 1k -
独立性检验用于确定两个变量之间是否存在统计显著关系。在这种情况下,其检验统计量基于列联表,并服从具有自由度的 χ² 分布,其中行数和列数是此列联表中的行数和列数。这也是一个右尾测试。
(r - 1)(c - 1)rc
来自 F 分数的 p 值
最后,当您执行检验统计量服从 F 分布(也称为费雪-斯奈德科分布)的检验时,应使用该选项。F 分布的确切形状取决于两个自由度。F-score
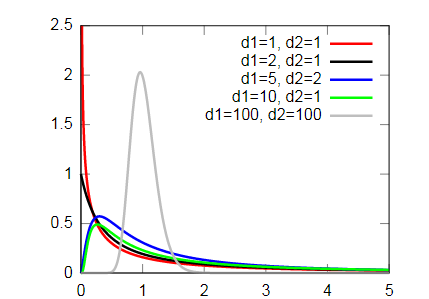
要了解这些自由度从何而来,请考虑自随机变量 and,它们分别遵循具有自由度的 χ² 分布。在这种情况下,比率服从 F 分布,具有自由度。因此,这两个参数也称为分子和分母自由度。XYd1d2(X/d1)/(Y/d2)(d1, d2)d1d2
F分数的 p 值由以下公式给出,其中我们表示 F 分布的累积分布函数,自由度:cdfF,d1,d2(d1, d2)
-
左尾F试验:
p-value = cdfF,d1,d2(Fscore) -
右尾 F 检验:
p-value = 1 - cdfF,d1,d2(Fscore) -
双尾 F 检验:
p-value